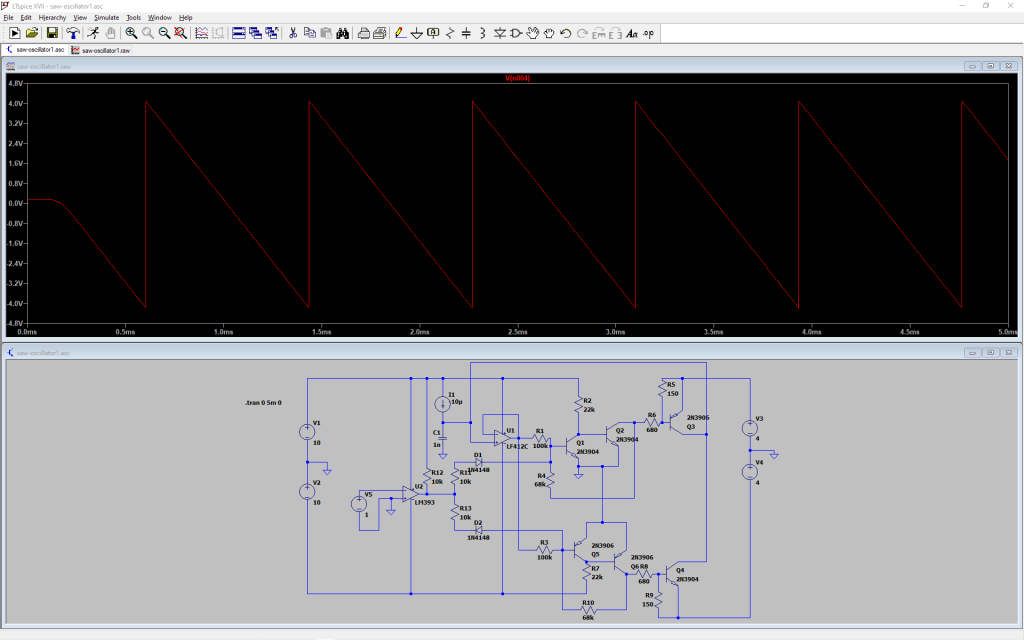
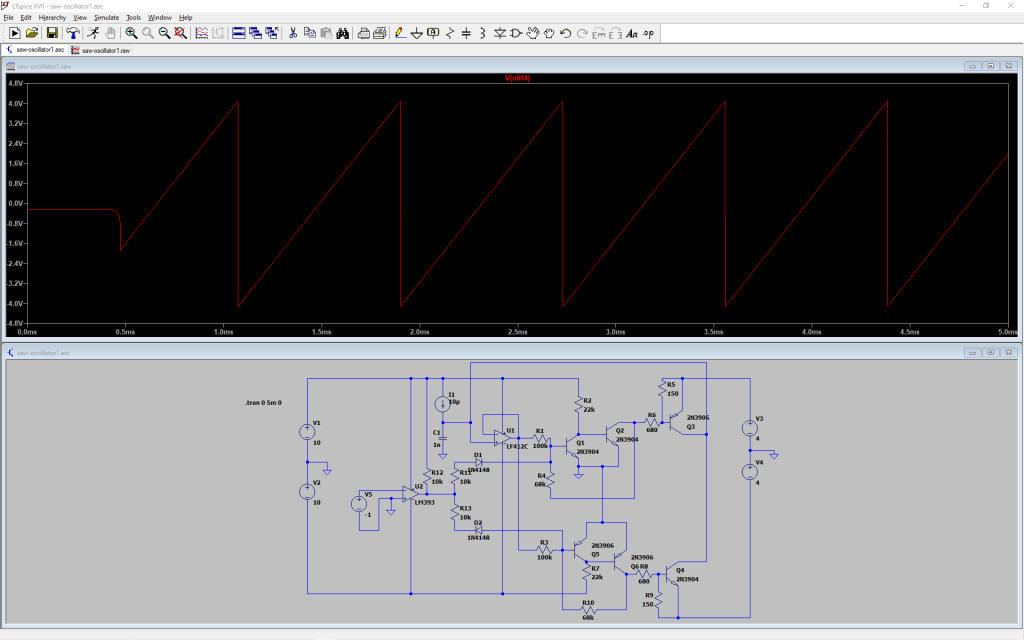
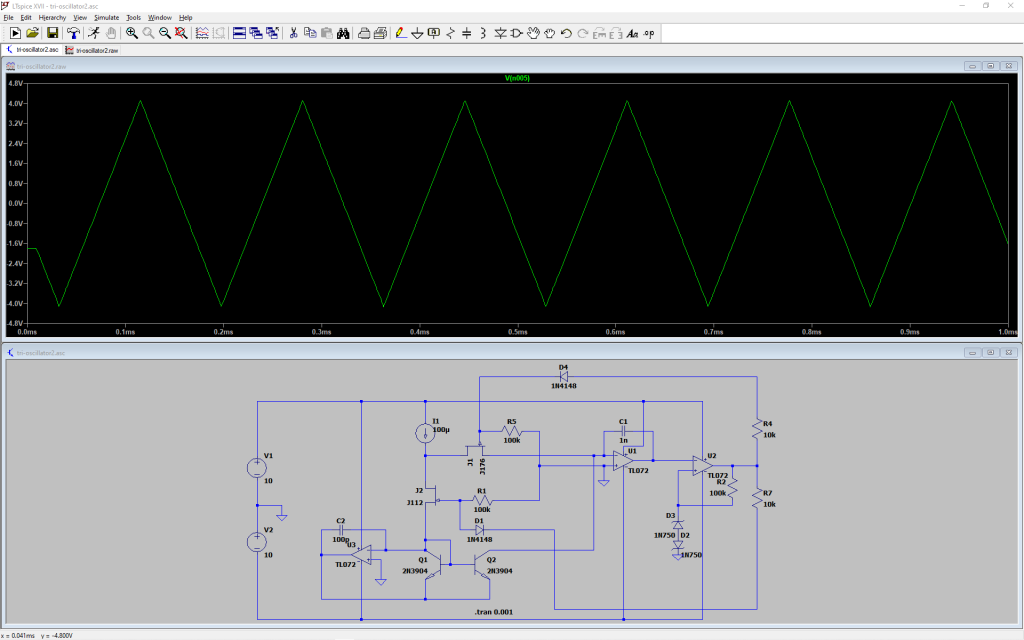
909クローンのファームウェアの開発中、eeprom に書き込んだリズムパタンが書き込んだ後に崩れる現象がまあまあ頻繁に発生して、最初はファームウェアのバグのせいかと思っていたのですが、バグにしてはどうにも発生場所がランダムだったり発生の契機が読めなかったりで、これはプロセッサの誤動作なのでは？と考え始め、発生条件をもっとよく調べてみたら、どうも電源を落として立ち上げると何の書き込みをしていなくてもちょいちょい壊れるらしい。そういうわけで何の問題でどう対策すれば良いのか調べました。
続きを読むTR-909 クローンのシーケンスパタンは eeprom に書き込みますが、avr-libc ライブラリが提供している eeprom 関数には同期書き込みしかありません。
https://www.nongnu.org/avr-libc/user-manual/group__avr__eeprom.html
しかし、TR-909 クローンのファームウェアでは割り込みをほとんど使わずリアルタイム処理がなされていて、eeprom を同期書き込みすると書き込み中処理が止まってしまいます。これが様々な誤動作の原因になってしまうので、非同期書き込み関数を書きました。
続きを読むThru-Zero FM ができる VCO を設計中ですが、前回ではシミュレータを使って思った通りに動きそうか確認しました。動きそうなので実際に回路を組んでみたいですが、シミュレーションではオシレータに入れる電流源は電流源モデルで済ませていたものの、実際には現実に動作する回路を入れないといけません。この電流源回路、正負逆転できるようにしないといけないんですがそんな電流源は組んだことがないのでそこもシミュレーションで動作確認してみました。下が回路図です。指数関数回路に OTA をつなげただけです。R1 と J1 で、約 200μA の定電流を発生していて、これで OTA 入力をバイアスしています。これがないと Linear CV の直線性が悪いので必須です。
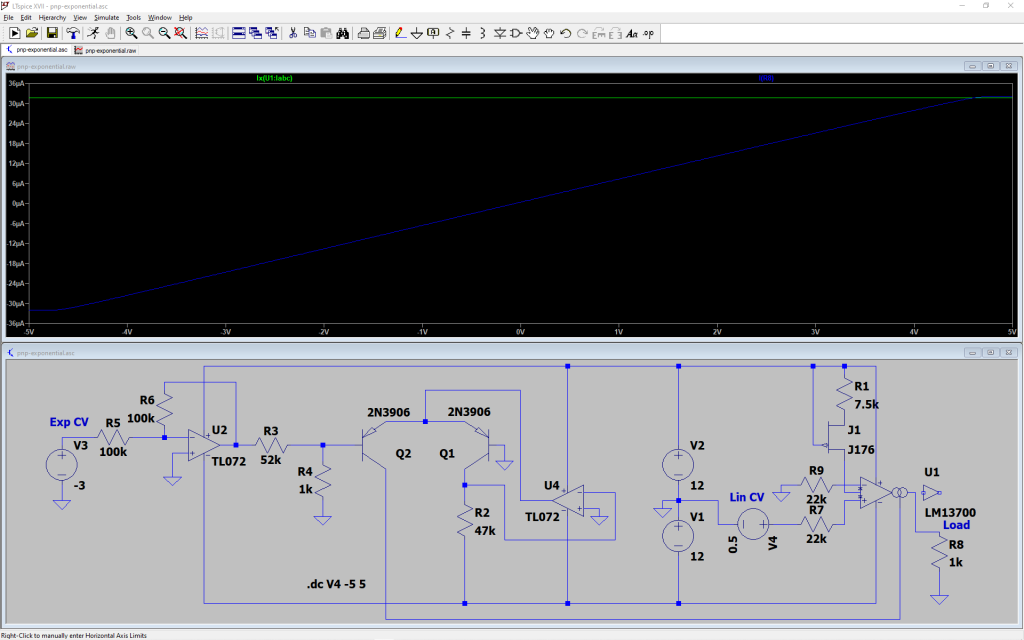
このカーブはリニア CV を変化したときの出力電流の変化です。緑線は OTA の Iabc で指数関数回路の出力につないであります。負の電流はきれいに出せるようですが、OTA の出力は Iabc を超えないので、定常時の Linear CV を注意深くとる必要がありそうです。
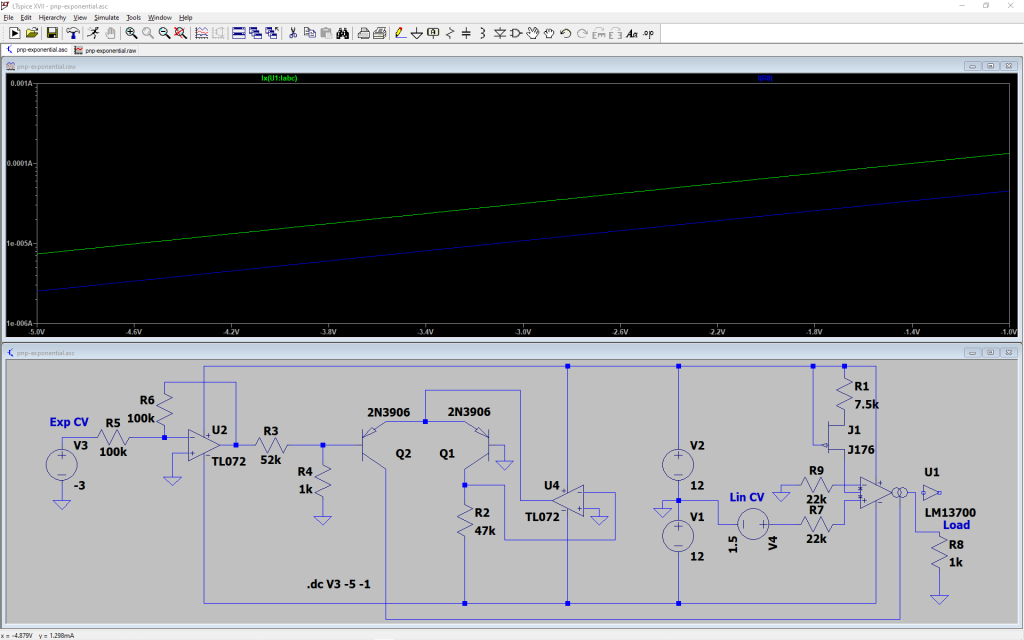
こちらは、Exponential CV を振った時の出力電流の挙動です。緑線が Iabc で青線が出力です。だいたい正確に対数軸上で平行を保っているので、周波数のトラッキングもできそうです。
ノコギリ波を発生するリセット型の VCO で Thru-Zero FM ができないかと考えてみました。極性の切り替えをしないといけないので外付けの制御が必要ですけれども電流の向きを逆転させて発振させることはできないことはなさそうです。
以下の図で、I1 と V5 の極性を逆転させると位相が反転します。
Quadrature Trapezoid VCO の続きです。Qadrature Trapezoid VCO は訳すと「直交台形波 VCO」みたいな感じです。元記事の回路図をこの記事に切り貼りするのはちょっとはばかられるので、解説、回路などは Donald さんの元記事を参照していただきたいですが、詳しい解説が書かれていてもそれでも難解な VCO なのでちょっと時間をかけて自分なりに理解してみました。この発振器、実に巧妙に設計されています。よく何もないところからこんな仕組みを思いついたなとすごく感心してしまいます。
続きを読む先日シミュレーションした CEM 3340 タイプの VCO ですが、スイッチング用 FET の片側を N チャンネルから P チャンネルに変えたら回路がずっと単純になるのでは？と気づき、やってみたところうまくゆくようです。
だいぶん単純になってきました。これはちょっと実際に回路を組んでみたいかも。ブレッドボード上でさくっと組めそうです。
VCO の再設計で一番やりたいことは、FM なのですが、アナログでやるのはかなり大変です。軽くかけるだけならアナログでも簡単にやれるのですが、ディジタル合成では簡単にできる「時間軸をさかのぼる」FM は、普通の伝統的な VCO では至難の業です。時間軸をさかのぼるということは、周波数をマイナスに持ってゆくということで、これは Thru-Zero FM と呼ばれているようです。電流を単方向にしか流せず、かつ時間軸上で非対称のノコギリ波を発生するリセット型の VCO では多分無理でしょう。三角波なら時間軸上で対称ですのでまだ目がありそうです。これについて、色々と調べてみたところ、二つの解決法が見つかりました。一つは、三角波からノコギリ波に変換するときに負の周波数では極性を反転する方法。これはまた後日記事にしたいと思います。もう一つは、Donald Tillman という人の考えた Quadrature Trapezoid VCO というタイプの VCO で、正負対称の電流を二つの積分器に流し込み、位相が90度ずれた二つの波形を作るというものです。もとアイデアの記事はこちらです。これは大変に面白いです。
ちょっと時刻が遅くなってしまったので続きは後日記事にします。
今汎用の VCO を作ろうかなと考えています。Analog2.0 の VCO も汎用なので今まで実験などに使ってきたのですけれども、調整箇所が多いなど色々と直したい点があるので一から作り直してみようと考えているわけです。
普通に作るなら今まで通りリセット型の発振器にするのが素直ですけれども、CEM3340 のような三角波を発生する VCO もかねてから興味があったので検討してみました。実は CEM 3340、今は入手しようと思えば入手できてしまいます。数を作るならそれを素直に使うのが良いかもしれないのですが、電源が ±15V と指定されています。利便性を考えて ±10V の電源で設計しようと考えているのでこのプロジェクトでは使えません。残念。昇圧するという手もあることはあるのですけれどもね。
続きを読む以前に、BOSS の DR-110 を改造して MIDI 信号を受けられるようにするというプロジェクトをじわじわやっていたのですが、
実はもうとっくに音が出るようになっていたのですが、こんな感じ
これは気持ち悪い。なんかリズムが転んでいる気がします。どうもおかしい。というところで、やる気が駄々下がりしてしまいかなり長いこと放置してしまいました。基板もむき出しで放ってあるので壊してしまいかねない。いい加減に収拾をつけないといけません。まずは本当にリズムが転んでいるかチェック。一番気持ち悪い二小節を切り出して、さらに波形を拡大してみると
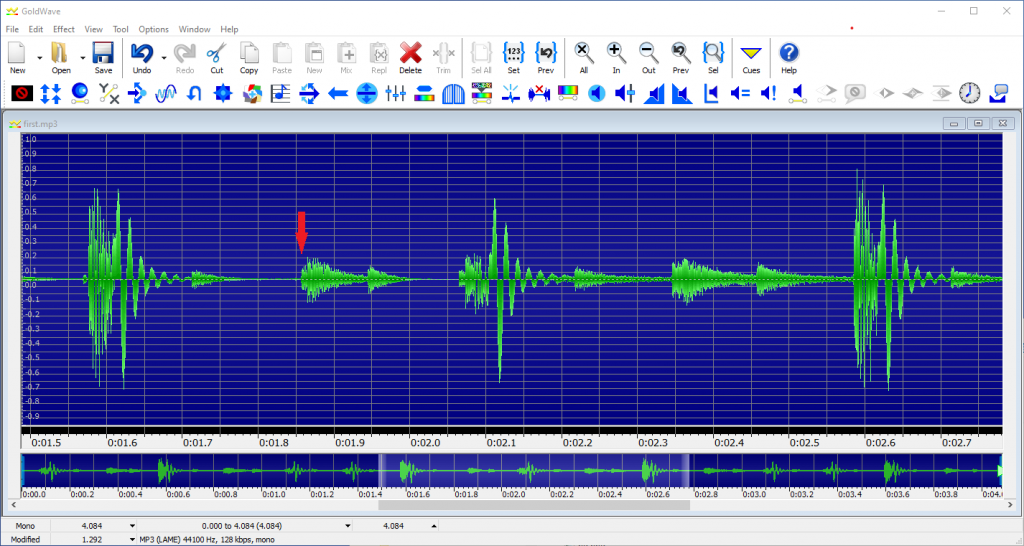
ああこれは。矢印のところは 16 ビートのハイハットですが、はっきり遅れています。それ以外の部分もどうもガタガタです。ざっと目測しただけですが本来欲しいタイミングより 40ms から 50ms ぐらい遅れている模様。こんな盛大な遅れが出るのはなぜかというのは謎が深いです。USB MIDI はフレームがあるのでジッタが出るという説もネットをあさっていて見かけました。この改造でも USB MIDI を使っていますが、仮に説が本当としても、USB MIDI のフレームサイズは 1ms なのでこの遅延は説明がつきません。そもそも 1ms ずれたぐらいでは人間にはわからないのではないでしょうか。まあとにかく、このままでは使い物になりません。
どうやって解決の糸口をつかむか思案しています。まずは MIDI 信号のタイミング測定からやってみようかな。
前回の記事で減衰時間から減衰率を求める計算式を考えましたが、K = e-0.01/T とかなり変な式、グラフを引いてみると、こんな風に極端な形で、この減衰率をマイクロプロセッサで求めるのはこれまた単純にはゆかなさそうです。
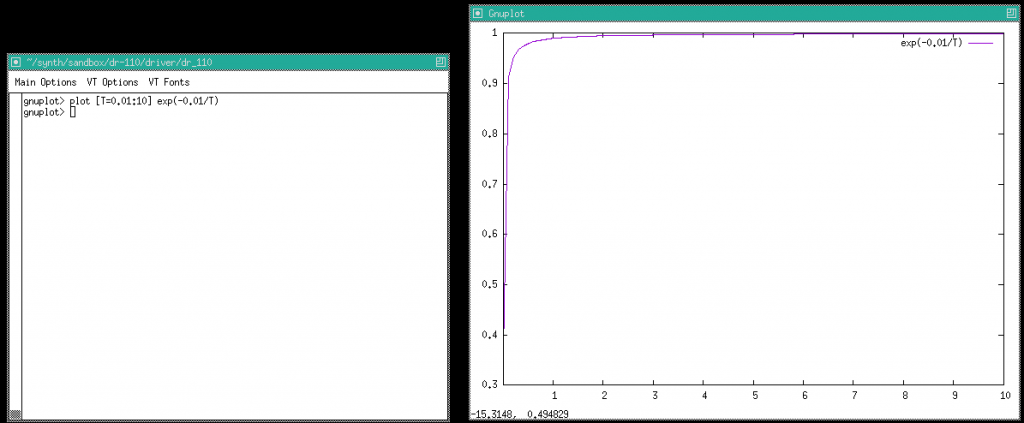
上記の式は非線形の関数なので、プロセッサで都度計算するのは時間がかかり、処理が追い付かなくなりそうです。近似値でよいので素早く計算したいです。手っ取り早いのはテーブル参照と補間・補外を使う方法、それなら実用的な速さで計算できそうです。
入力は、1024 ステップの整数値でこれを欲しい減衰時間に線形に対応させます。出力はその減衰時間のための減衰率です。テーブルには主要の入力値にたいする減衰率を覚えさせます。
ただここで一つ問題が。参照テーブルの値の精度をどれぐらい取る必要があるか試行錯誤しましたが、今の僕の技術ではどうしても 32bit 必要です。これを 1024 点全部覚えさせるには、1024 x 4 = 4KB の SRAM が必要です。今プロセッサに AVR の ATmega168 を使っていますが、内部 SRAM が 1KB しかありません。思い切りあふれています。テーブルの点数を 256 点にして補間しましたが変化が急激すぎて時間分解能が足りません。それでもまだメモリがあふれています。テーブルの作りに工夫が必要です。
その前に、まず時間変化の範囲をどれぐらいに取る必要があるか決めました。これは音を出して決めるのが一番、パラメータを変え、音を聞きを繰り返して、多分時定数を 1ms から 5s の範囲で動かせれば十分なようです。いずれもっと長い立ち上がりと減衰が欲しくなるかもしれませんが、まあ将来の改良点ということにしてほっときます。
で、もう一度上のグラフを見ると、カーブが急激に動くのはせいぜい 1 秒ぐらいまでで、あとはほぼ横ばいです。なので、時間の短いところと長いところでテーブルの時間分解能を変えるのはどうでしょうか？目標は 128点。これで 512B のサイズで、メモリには余裕ができます。
これまた試行錯誤して、最初の 64 点 (0.3秒ぐらいまで) は入力値とテーブルを一対一で対応して、残りの 1024 – 64 = 960 点は時間分解能がそれほど必要ないのでテーブルの後半のもう 64 点でカバーしてみると、かなり良い精度で近似できました。後半はテーブル一点で入力値の15点をまかなう計算になります。それだと値がカクカクするから線形に補完します。
テーブルの値の計算をするプログラムはこちら。ちょっと雑なプログラムですけどまあさっと動かしてしまいたかったので。テーブルの値は、Q0.32 の固定小数点数です。減衰率なので値は絶対に 1 未満なのでこれで大丈夫です。
#include <math.h>
#include <stdint.h>
#include <stdio.h>
uint32_t table[128];
int main(int argc, char *argv[]) {
for (int i = 0; i < 1024; ++i) {
if (i >= 64 && (i - 64) % 15 != 0) {
continue;
}
double x = -0.0001 / (0.001 + 5.0 * i / 1024.0);
uint32_t value = ((uint32_t) (exp(x) * (float) ((uint64_t) 1 << 32)));
int index = (i < 64) ? i : ((i - 64) / 15 + 64);
table[index] = value;
printf("%12u,", table[index]);
if (index % 4 == 3) {
printf("\n");
}
}
return 0;
}
このプログラムで作ったテーブルをマイクロプロセッサに埋め込んで減衰率を求める関数を書きました。今のところ良好です。
/*
* Exponential decay/grow ratio lookup table.
*
* The table stores data points to give decay/grow ratio for lookup keys ranging
* from 0 to 1023 (inclusive). The key 0 receives the ratio for time constant
* 0.001s (1ms) approximately. The key 1023 receives the ratio for time constant
* about 5s. The values in th table are Q0.32 unsigned fixed point numbers.
*
* In order to save data memory space, the values have different key resolutions
* depending on the position in the table.
* Table values with indexes from 0 to 63 has 1-1 key mapping to index,
* i.e.
* ratio = kTransientRatios[key]
* But for the indexes from 64 to 127, the table keeps only values for every 15 keys,
* i.e.
* ratio = kTransientRatios[(key - 64) / 15 + 64]
* where (key - 64) % 15 == 0
*
* Ratios for keys that are not on these indexes need to be calculated
* by interpolation or extrapolation. See the method GetRatio().
*/
uint32_t kTransientRatios[128] = {
3886247118, 4222575580, 4255256816, 4267608186,
4274098987, 4278100538, 4280814394, 4282775974,
4284259997, 4285421933, 4286356375, 4287124175,
4287766262, 4288311174, 4288779419, 4289186113,
4289542645, 4289857756, 4290138268, 4290389583,
4290616034, 4290821137, 4291007774, 4291178333,
4291334804, 4291478865, 4291611934, 4291735225,
4291849776, 4291956486, 4292056132, 4292149393,
4292236865, 4292319070, 4292396469, 4292469473,
4292538445, 4292603710, 4292665560, 4292724255,
4292780031, 4292833101, 4292883656, 4292931872,
4292977906, 4293021905, 4293063999, 4293104310,
4293142949, 4293180018, 4293215611, 4293249813,
4293282706, 4293314362, 4293344850, 4293374234,
4293402573, 4293429921, 4293456330, 4293481846,
4293506515, 4293530379, 4293553475, 4293575840,
4293597508, 4293856889, 4294033677, 4294161903,
4294259161, 4294335461, 4294396917, 4294447478,
4294489805, 4294525758, 4294556676, 4294583547,
4294607117, 4294627960, 4294646522, 4294663159,
4294678155, 4294691742, 4294704109, 4294715414,
4294725787, 4294735340, 4294744166, 4294752345,
4294759946, 4294767027, 4294773641, 4294779831,
4294785639, 4294791097, 4294796237, 4294801085,
4294805667, 4294810002, 4294814111, 4294818011,
4294821717, 4294825243, 4294828603, 4294831807,
4294834867, 4294837792, 4294840590, 4294843270,
4294845839, 4294848303, 4294850670, 4294852944,
4294855131, 4294857236, 4294859264, 4294861218,
4294863103, 4294864922, 4294866678, 4294868376,
4294870017, 4294871604, 4294873141, 4294874628,
4294876070, 4294877467, 4294878823, 4294880138,
};
uint32_t GetRatio(uint16_t key) {
const int kTableBoundary = 64;
if (key < kTableBoundary) {
return kTransientRatios[key];
}
const int kResolution = 15;
int index = (key - kTableBoundary) / kResolution + kTableBoundary;
int ramainder = (key - kTableBoundary) % kResolution;
register uint32_t temp = kTransientRatios[index];
if (ramainder > 0) {
register uint32_t temp2;
if (index == 127) {
temp2 = temp - kTransientRatios[index - 1];
} else {
temp2 = kTransientRatios[index + 1] - temp;
}
temp2 *= ramainder;
temp2 /= kResolution;
temp += temp2;
}
return temp;
}