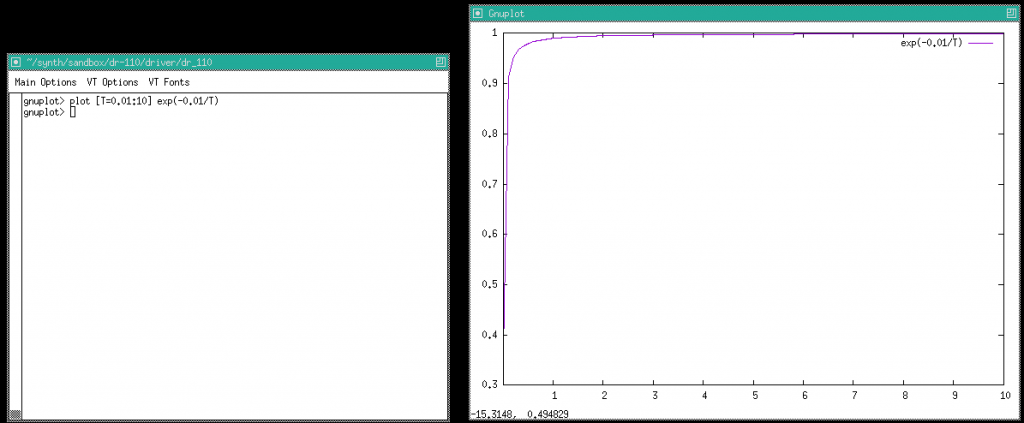
前回の記事で減衰時間から減衰率を求める計算式を考えましたが、K = e-0.01/T とかなり変な式、グラフを引いてみると、こんな風に極端な形で、この減衰率をマイクロプロセッサで求めるのはこれまた単純にはゆかなさそうです。
上記の式は非線形の関数なので、プロセッサで都度計算するのは時間がかかり、処理が追い付かなくなりそうです。近似値でよいので素早く計算したいです。手っ取り早いのはテーブル参照と補間・補外を使う方法、それなら実用的な速さで計算できそうです。
入力は、1024 ステップの整数値でこれを欲しい減衰時間に線形に対応させます。出力はその減衰時間のための減衰率です。テーブルには主要の入力値にたいする減衰率を覚えさせます。
ただここで一つ問題が。参照テーブルの値の精度をどれぐらい取る必要があるか試行錯誤しましたが、今の僕の技術ではどうしても 32bit 必要です。これを 1024 点全部覚えさせるには、1024 x 4 = 4KB の SRAM が必要です。今プロセッサに AVR の ATmega168 を使っていますが、内部 SRAM が 1KB しかありません。思い切りあふれています。テーブルの点数を 256 点にして補間しましたが変化が急激すぎて時間分解能が足りません。それでもまだメモリがあふれています。テーブルの作りに工夫が必要です。
その前に、まず時間変化の範囲をどれぐらいに取る必要があるか決めました。これは音を出して決めるのが一番、パラメータを変え、音を聞きを繰り返して、多分時定数を 1ms から 5s の範囲で動かせれば十分なようです。いずれもっと長い立ち上がりと減衰が欲しくなるかもしれませんが、まあ将来の改良点ということにしてほっときます。
で、もう一度上のグラフを見ると、カーブが急激に動くのはせいぜい 1 秒ぐらいまでで、あとはほぼ横ばいです。なので、時間の短いところと長いところでテーブルの時間分解能を変えるのはどうでしょうか?目標は 128点。これで 512B のサイズで、メモリには余裕ができます。
これまた試行錯誤して、最初の 64 点 (0.3秒ぐらいまで) は入力値とテーブルを一対一で対応して、残りの 1024 – 64 = 960 点は時間分解能がそれほど必要ないのでテーブルの後半のもう 64 点でカバーしてみると、かなり良い精度で近似できました。後半はテーブル一点で入力値の15点をまかなう計算になります。それだと値がカクカクするから線形に補完します。
テーブルの値の計算をするプログラムはこちら。ちょっと雑なプログラムですけどまあさっと動かしてしまいたかったので。テーブルの値は、Q0.32 の固定小数点数です。減衰率なので値は絶対に 1 未満なのでこれで大丈夫です。
#include <math.h>
#include <stdint.h>
#include <stdio.h>
uint32_t table[128];
int main(int argc, char *argv[]) {
for (int i = 0; i < 1024; ++i) {
if (i >= 64 && (i - 64) % 15 != 0) {
continue;
}
double x = -0.0001 / (0.001 + 5.0 * i / 1024.0);
uint32_t value = ((uint32_t) (exp(x) * (float) ((uint64_t) 1 << 32)));
int index = (i < 64) ? i : ((i - 64) / 15 + 64);
table[index] = value;
printf("%12u,", table[index]);
if (index % 4 == 3) {
printf("\n");
}
}
return 0;
}このプログラムで作ったテーブルをマイクロプロセッサに埋め込んで減衰率を求める関数を書きました。今のところ良好です。
/*
* Exponential decay/grow ratio lookup table.
*
* The table stores data points to give decay/grow ratio for lookup keys ranging
* from 0 to 1023 (inclusive). The key 0 receives the ratio for time constant
* 0.001s (1ms) approximately. The key 1023 receives the ratio for time constant
* about 5s. The values in th table are Q0.32 unsigned fixed point numbers.
*
* In order to save data memory space, the values have different key resolutions
* depending on the position in the table.
* Table values with indexes from 0 to 63 has 1-1 key mapping to index,
* i.e.
* ratio = kTransientRatios[key]
* But for the indexes from 64 to 127, the table keeps only values for every 15 keys,
* i.e.
* ratio = kTransientRatios[(key - 64) / 15 + 64]
* where (key - 64) % 15 == 0
*
* Ratios for keys that are not on these indexes need to be calculated
* by interpolation or extrapolation. See the method GetRatio().
*/
uint32_t kTransientRatios[128] = {
3886247118, 4222575580, 4255256816, 4267608186,
4274098987, 4278100538, 4280814394, 4282775974,
4284259997, 4285421933, 4286356375, 4287124175,
4287766262, 4288311174, 4288779419, 4289186113,
4289542645, 4289857756, 4290138268, 4290389583,
4290616034, 4290821137, 4291007774, 4291178333,
4291334804, 4291478865, 4291611934, 4291735225,
4291849776, 4291956486, 4292056132, 4292149393,
4292236865, 4292319070, 4292396469, 4292469473,
4292538445, 4292603710, 4292665560, 4292724255,
4292780031, 4292833101, 4292883656, 4292931872,
4292977906, 4293021905, 4293063999, 4293104310,
4293142949, 4293180018, 4293215611, 4293249813,
4293282706, 4293314362, 4293344850, 4293374234,
4293402573, 4293429921, 4293456330, 4293481846,
4293506515, 4293530379, 4293553475, 4293575840,
4293597508, 4293856889, 4294033677, 4294161903,
4294259161, 4294335461, 4294396917, 4294447478,
4294489805, 4294525758, 4294556676, 4294583547,
4294607117, 4294627960, 4294646522, 4294663159,
4294678155, 4294691742, 4294704109, 4294715414,
4294725787, 4294735340, 4294744166, 4294752345,
4294759946, 4294767027, 4294773641, 4294779831,
4294785639, 4294791097, 4294796237, 4294801085,
4294805667, 4294810002, 4294814111, 4294818011,
4294821717, 4294825243, 4294828603, 4294831807,
4294834867, 4294837792, 4294840590, 4294843270,
4294845839, 4294848303, 4294850670, 4294852944,
4294855131, 4294857236, 4294859264, 4294861218,
4294863103, 4294864922, 4294866678, 4294868376,
4294870017, 4294871604, 4294873141, 4294874628,
4294876070, 4294877467, 4294878823, 4294880138,
};
uint32_t GetRatio(uint16_t key) {
const int kTableBoundary = 64;
if (key < kTableBoundary) {
return kTransientRatios[key];
}
const int kResolution = 15;
int index = (key - kTableBoundary) / kResolution + kTableBoundary;
int ramainder = (key - kTableBoundary) % kResolution;
register uint32_t temp = kTransientRatios[index];
if (ramainder > 0) {
register uint32_t temp2;
if (index == 127) {
temp2 = temp - kTransientRatios[index - 1];
} else {
temp2 = kTransientRatios[index + 1] - temp;
}
temp2 *= ramainder;
temp2 /= kResolution;
temp += temp2;
}
return temp;
}
