エンベロープジェネレータのプログラムですが、現状は指数関数テーブルを参照して出発点の値に時間ごとに減衰する指数関数を掛け合わせて減衰曲線を作っています。

https://github.com/naokiiwakami/vceg

これは精度をあまり気にせずにざっと計算できるので手っ取り早いのですが、プログラムはどうしても煩雑になります。また、値の更新周期は約 10ms なのですが、減衰が遅いと 10ms の間には値が動かず、時間軸を補間しないといけません。これはまだ実装していませんがプログラムはもっと煩雑になります。

ちょっと嫌だなと考え始めたのですが、そもそも指数関数の減衰は

V(i+1) = V(i) * k

where 0 <= k < 1

のような式で簡単に作れそうなものなのですが、実はそう甘くはありません。例えば、1秒で半分に減衰する曲線を、10ms の更新周期で計算しようとすると、k の値は

k = 0.5 ^ (1 / 100) = 0.99309249543703590153321021688807

限りなく 1 に近いけれども 1 にしてしまったら減衰しません。変数として float を使えばいいじゃない？とも思いますが、例えば AVR で float を static 領域に持つとなんだかわからないけれどもデータがばんばん壊れてしまいます（バグかもしれませんが）。それにそもそもふつうのマイクロプロセッサでの浮動小数点演算は遅いです。ということで、固定小数点演算で曲線が求まらないか考えてみました。

ブランクがあまりにも長いのでやり方を忘れてしまいました。ので調べました。以下の解説がとてもわかりやすかったです

https://www.allaboutcircuits.com/technical-articles/multiplication-examples-using-the-fixed-point-representation/

いつか上記リンク先がなくなってしまうかもしれないので解説を書いとくのも良いのですが、何分もう夜分遅いので、書いたプログラムだけだっと貼っちゃいます。

#include <stdio.h>
#include <stdint.h>

int main(int argc, char *argv[]) {
  // fixed point integer 10bit.6bit
  uint16_t value = (1023) << 6;
  // fixed point integer .16bit
  uint16_t decay_factor = 0.99309249543703590153321021688807 * 65536;
  for (uint16_t i = 0; i < 1000; ++i) {
    // multiplication
    uint32_t temp = value * decay_factor;
    value = temp >> 16;
    // retrieve the integer part
    uint16_t output = value >> 6;
    printf("%d %d\n", i, output, 10);
  }
  return 0;
}

結果もさくっと貼っちゃいます

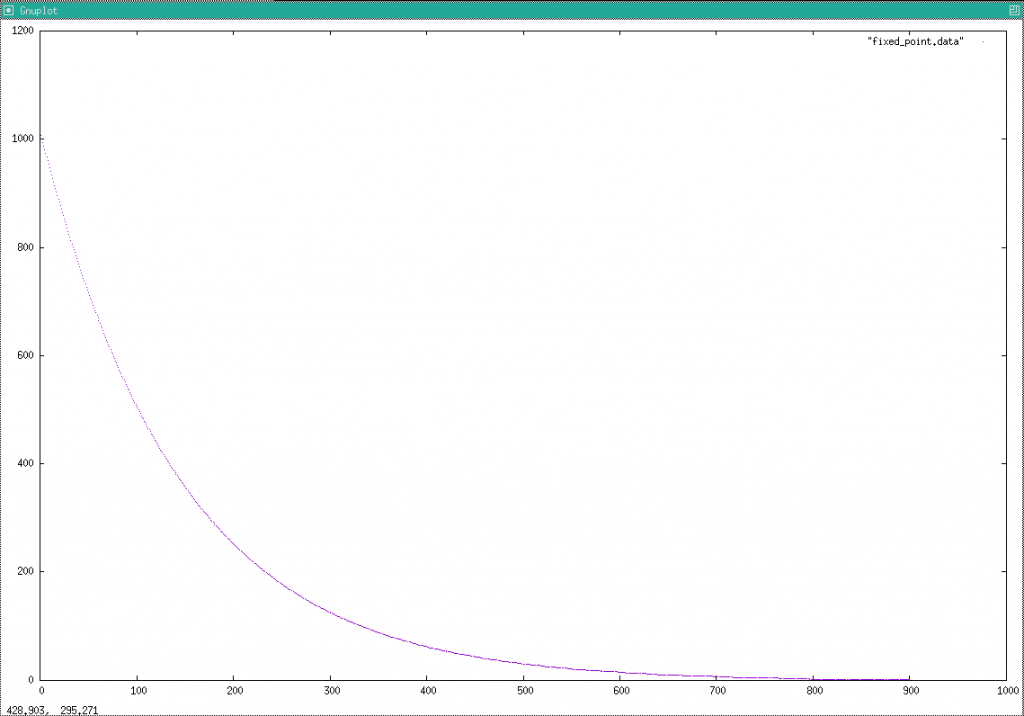
これはいけそうな気がします。