エンベロープジェネレータの減衰曲線は、単純な指数曲線ではなく、時間とともに減衰率を変えて行くとより自然な減衰が得られるという検討について以前記事に書きました。その記事ではアタック直後の減衰では振幅に応じて減衰率を下げて速くレベルを落とす方法を試しました。出音は良いと感じたものの調整はかなり難しく、また、必要な演算量も大きく、もう少し単純で直感的な方法はないのかな?と思案していたのですが、散歩している最中にふと、コンデンサへの充放電を模してみたら単純にならないかな?と思いつきました。
下の図は RC 回路の放電の様子を描いたものですが、その減衰が指数曲線を描くのはどういうわけかというと、コンデンサから流れ出る電流は Vout / R で決まる。Vout は時々刻々と変わるが、非常に短い時間間隔 Δt の区間 Vout が一定だと考えると、電流も一定、その間放出される電荷は Vout x Δt / R となり、Vout に比例した電荷が放出されることになります。電荷の放出により Vout の降下分は Vout x Δt x C / R ここから指数関数を導き出す方法は忘れてしまったのですが、感覚的には Vout が大きいときは速く減衰してゆき、Vout が小さくなると電荷の放出も小さくなるので減衰が遅くなるのがわかります。
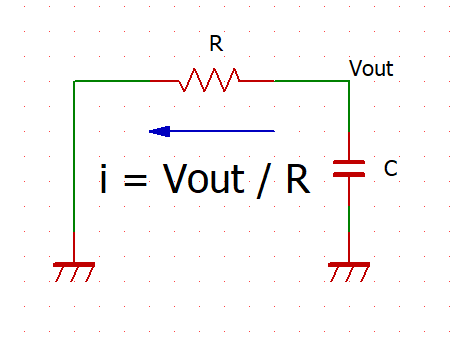
この記事では、指数関数を導き出すのはあまり重要ではなく、むしろ Vout を求める式
が重要です。計算を単純にするために CΔt の定数を 1 とすると
と、非常に単純な式になります。減衰率を使った計算では、適切な減衰率を計算するのが重たかったのですが、上式では、RC 回路の R の値をそのまま使っています。C が一定だとすると、回路の時定数は R に比例することがわかっていますから、R の値を決めるのは比較的単純です。上の計算式も複雑な演算を必要としません。これで減衰曲線を計算できるならこっちの方式の方が便利な点が多いんじゃないでしょうか?
ということで、python でお試しプログラムを書いてみました。
voltage = 1.0
resistance = 60000
for index in range(200000):
print(f"{index} {voltage}")
voltage -= voltage / resistance拍子抜けするぐらい簡単なプログラムですが。出力はこうなります。これは、いい感じなのではないでしょうか?
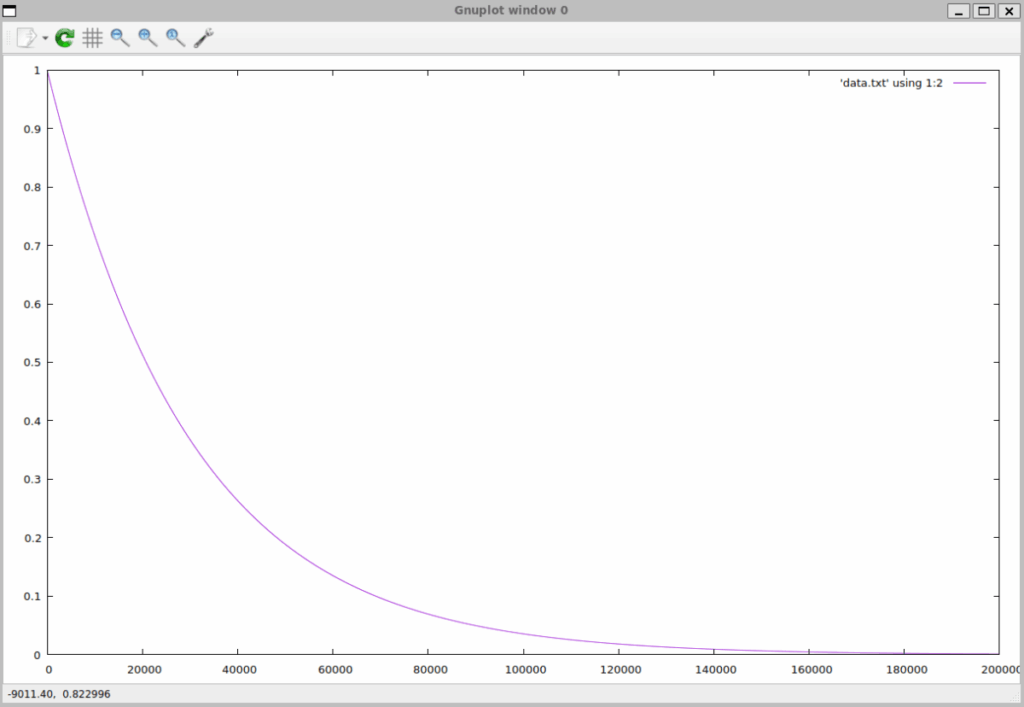
試しに対数軸にプロットしてみます。やはり良いですね
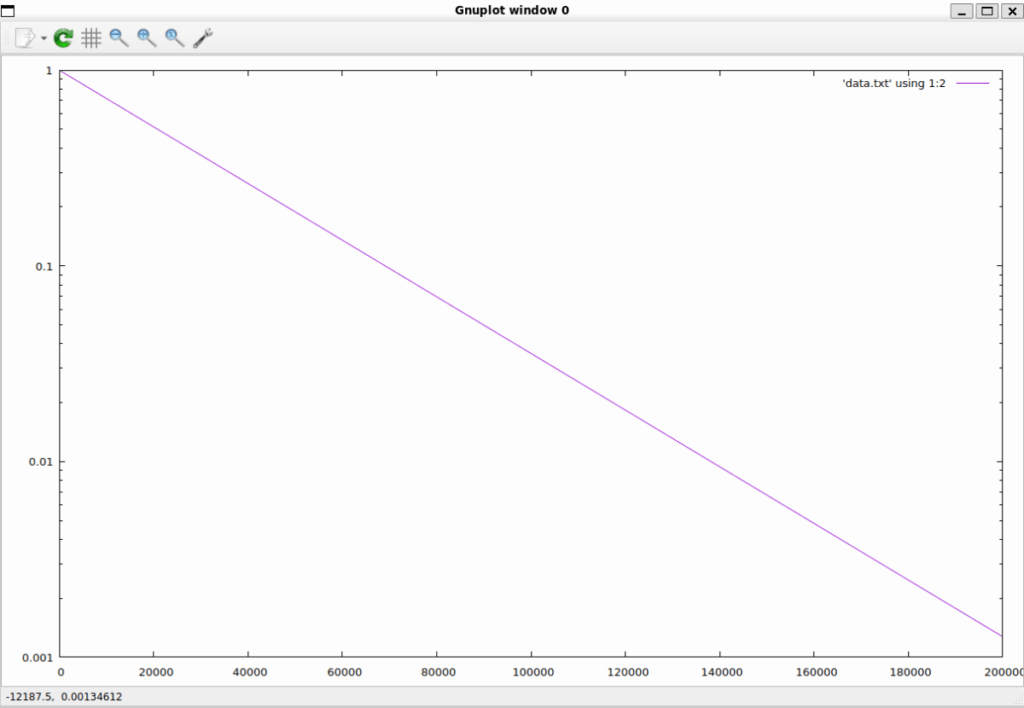
R を変えると時定数が変わるか確認してみます。
voltage_a = 1.0
voltage_b = 1.0
resistance_a = 30000
resistance_b = 60000
for index in range(200000):
print(f"{index} {voltage_a} {voltage_b}")
voltage_a -= voltage_a / resistance_a
voltage_b -= voltage_b / resistance_b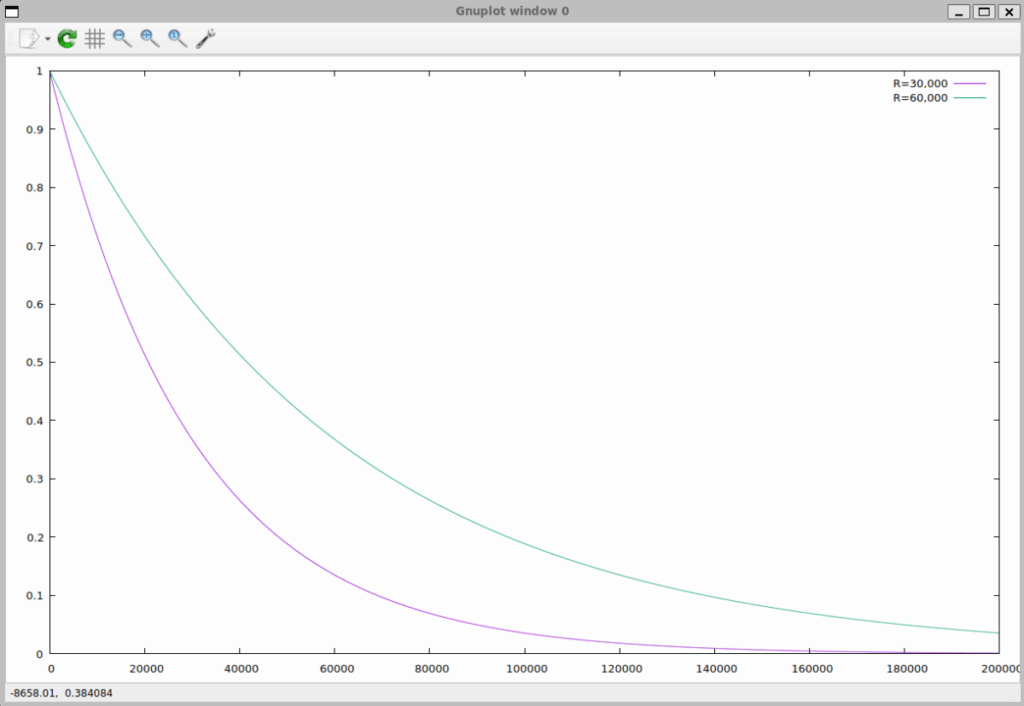
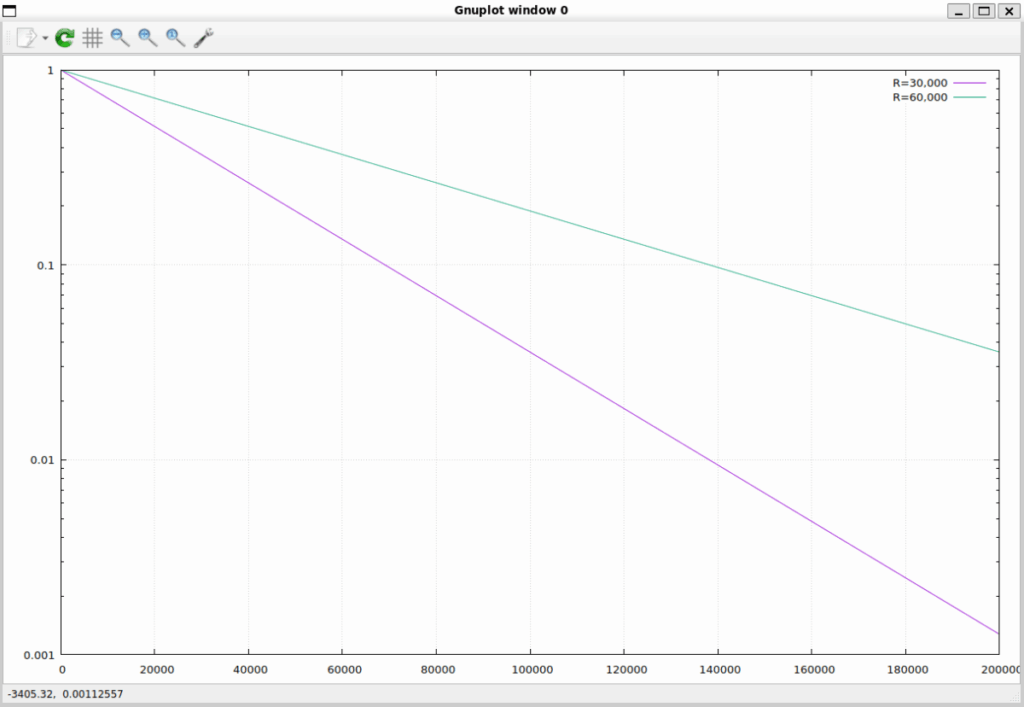
いいですね。R と時定数は理論通り比例しています。
アタック直後の減衰を速めるにはどうしたらよいでしょうか?試しにこんなコードを組んでみました。
voltage_a = 1.0
voltage_b = 1.0
voltage_c = 1.0
resistance_a = 30000
resistance_b = 60000
resistance_c = 90000
for index in range(200000):
print(f"{index} {voltage_a} {voltage_b} {voltage_c}")
voltage_a -= voltage_a / resistance_a
voltage_b -= voltage_b / resistance_b
if voltage_c < 0.5:
voltage_c -= voltage_c / resistance_c
else:
voltage_c -= voltage_c / resistance_c * (1.0 + (voltage_c - 0.5) * 4.0)0.5 よりも出力レベルが高いときには、出力レベルに応じて時定数が小さくなるように組んでいます。0.5 より低いときには単純な指数関数になるはず。狙いは現行の方式と同じですが、こちらの方がはるかに単純な演算で済みます。
結果以下のような曲線が得られました。アタック直後は R=30,000 の曲線に近いですが、徐々に伸び最後には R=60,000 よりもゆっくりな減衰になります。
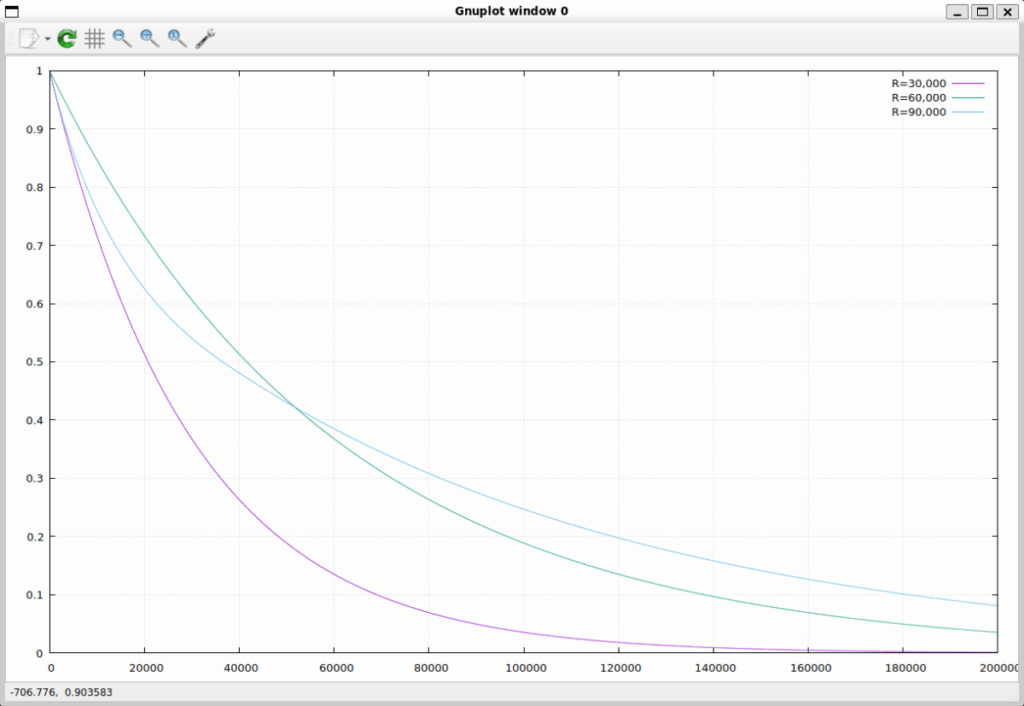
対数軸で見てみると、曲線がどうゆがんでいるのか見やすくなります。
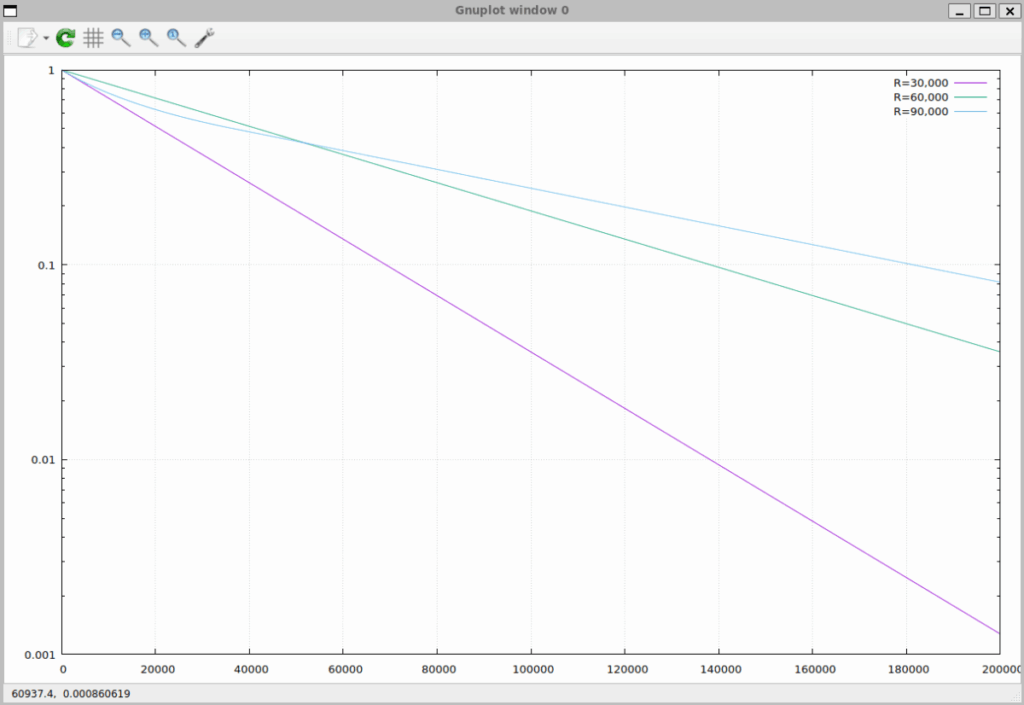
まだ机上検討段階ですが、好感触です。
