前回の記事では、モールス信号の読み取りに迷ったらどちらの可能性にも分岐する「多重世界線方式」を考えて実装したところ、その自信度で評価して一番上に正解が来るようになりました。しかし可能性をいくつも見せても仕方がないのでやはり一つを残して他は刈り取る必要があります。これが次の課題です。
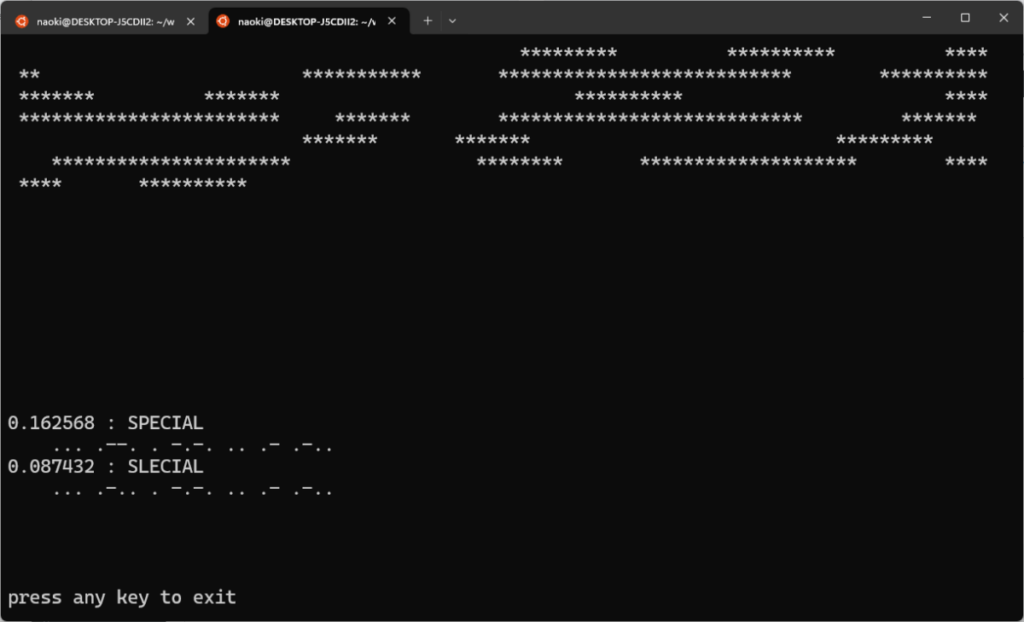
ここで「自信度」が役に立ちそうです。世界線の遷移を見てみると、最後まで生き残るパタンの場合、相対的な自信度は動かないようです。これは説明がつきそうです。冒頭に出した SPECIAL の例を見てみると
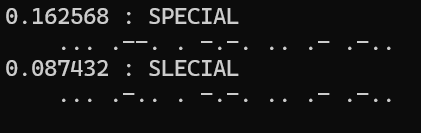
二文字目で二つの可能性 .--. (P) と.-.. (L) に分岐してその後は同じ認識結果です。自信度は分岐の時だけ変わるので、枝分かれした後ずっと平行線をたどったわけです。これで二番目以降を刈り取るにはどうしましょう？
例えば上のようなパタンの場合、一旦できた自信度の格差は縮まる可能性がありません。実際分岐したところで「間違い」はもう確定しているからです。つまり、自信度の格差は一般的に回復しないので引きずっても意味がないと予想されます。ならば、引きずれないようにしてしまいましょう。名づけて「いったんついた格差は容赦なく開く方式」
どうするか？単純にこういう風にしてみました
- モールス信号が立ち上がった時と立ち下がった時に全世界線を更新した後、自信度を2乗する
- 自信度がトップの 1/8 になったらもう望みなし、終了
これだけ？と思うかもしれませんが、コンピュータサイエンスでの2乗の破壊力はすさまじいものがあります。2乗を繰り返すわけですからその次には4乗、さらに次は 8乗と、格差はあっという間に爆発的に増えることになります。はっきり言ってちょっと乱暴にやりすぎ、1.5 乗とかにしたら？とも思いましたが、多分回復するのはトップが破綻するときぐらい、それは非常に短いサイクルで起こるだろうし、1.5 乗とか演算が重たいし、まずはいっちゃいましょう
ということでやってみました。2乗を繰り返すと自信度がアンダーフローしかねないので毎回トップの値が 1.0 になるように正規化しています。
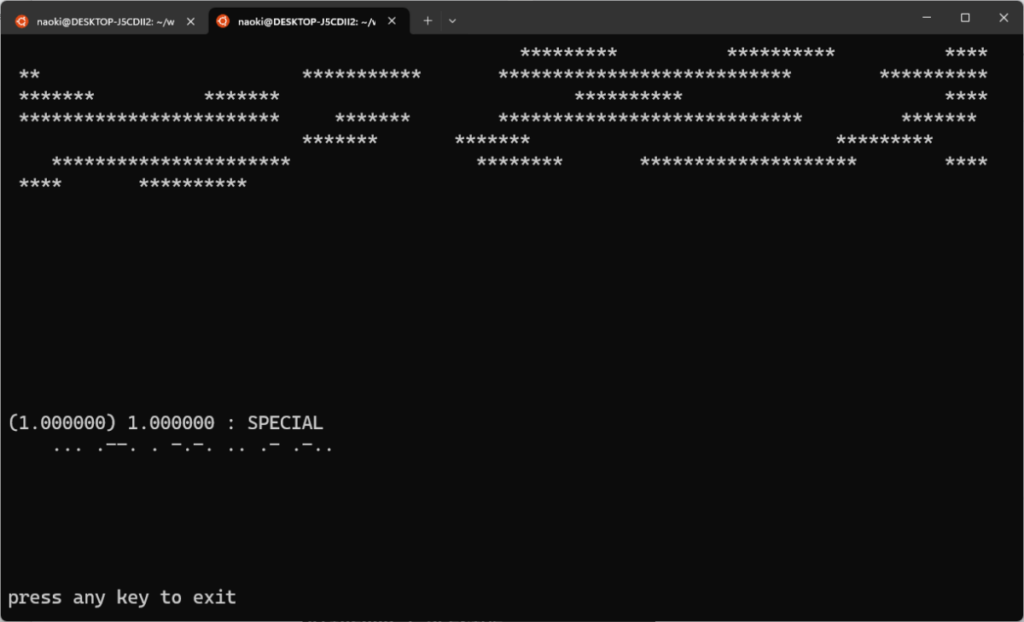
いけた？別のテスト入力で試してみましょう。
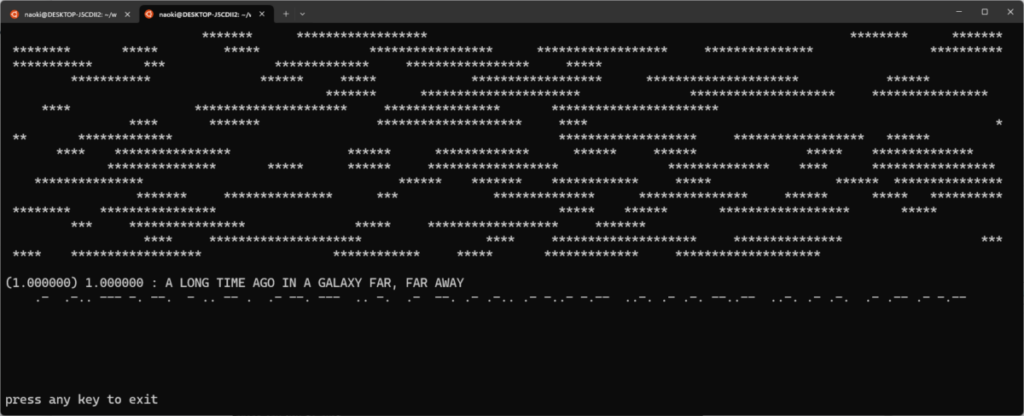
まじか。あれほどたくさんあった枝が一本に。しかもちゃんと正解を拾ってます。思いついといて実装しといてなんだけど、こんな乱暴なのでいいの？
いくつか他のサンプルも試してみて、やはりあまりに乱暴すぎることはわかりました。効きが強すぎて、挙動が不安定な立ち上がり時に必要な可能性まで刈り取ってしまいます。そういうことで、立ち上がってしばらくは自信度の2乗はやらないことにしました。これまた雑なやり方ですけどとりあえず手持ちのテストパタンはすべて正解に絞れるようになりました。
今のところ結果は画面表示しているだけできちんと出力の形になっていませんがそれは後でやるとして、パタン認識はここまで。まだもう一つ大きな懸念事項、入力のノイズ除去があるからです。
コードの履歴と最新は github で見られます
https://github.com/naokiiwakami/morse-code-reader
