なおもしつこくアンチログ回路を勉強中です。
Minimoog の VCF に使われているアンチログ回路を切り出してきて特性を測ってみました。
実験回路はこんな感じです。回路定数は Minimoog そのままではありません。この回路は他にも Takeda さんのページにあるTB-VCOなどでも使われています。(すみません勝手にリンクを張ってしまいました)
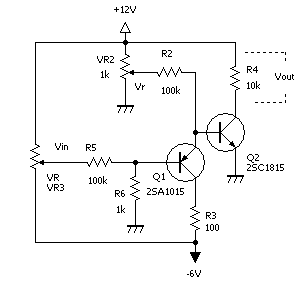
これも解析してみたられっきとした温度補償つき回路でした。解析の過程は長くなるので省略しますが、結果として以下のような関数が得られました。
Vout = (R4/R2) * Vr * exp(q/kT * Vin)
解析には、R5, R6による電圧降下を入れていないので、測定の絶対値はこの式からは取れません。
この回路で Vr を振って Vin = -2 ~ 2V で測定した結果が以下です。Vout の単位は mV です。2オクターブ強ぐらいの測定範囲ですが、かなりきれいに指数関数近似されています。(もっと曲がるものだと思い込んでいました)Vr は、Minimoog の回路図などでは Range の調整としてかかれています。図を見ると確かに対数軸上で並行移動しているので、Range の調整になることがわかります。解析式からもわかるはずですがグラフを見るまで理解できませんでした。
さて、これでアンチログ回路恐怖症がかなり薄れてきたのでいいかげんに VCF 製作にかかりたいと思います。
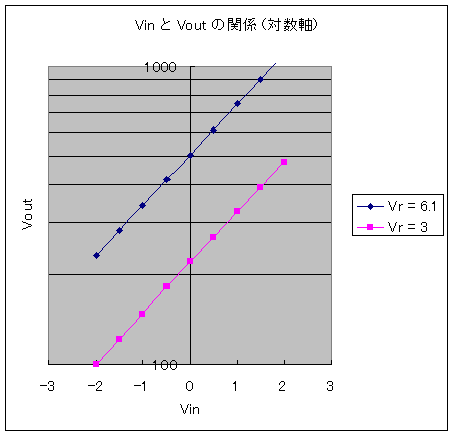






ちなみに scale 調整は R5 と R6 の比でやるようです。0.3%/℃の温度補償は R6 でやればよいはずですね。
式中の Vrの項は (Vr-Vbe2)のような気もしますが?…
またQ1のIcは OPAMPのantilogと異なり温度変化で多少変動しますので温度変化によるQ1のVbeの変化(温度補償動作)はOP AMPのantilogの場合より原理的には
小さく(弱く)なります。
この回路の場合、温度でIc1が動かないとVbe1の変動分とR2*Ieの変動分のつじつまが合わないのでIc1は必然的に動いて両者の変動がバランスするところ( 温度変化によるVbe-Ic曲線を満たす点 )で収まる。これすなわちNFBによるエミッタフォロワ回路のIcの変動率の改善そのものなわけです。
こちらもコメントありがとうございます。
> 式中の Vrの項は (Vr-Vbe2)のような気もしますが?…
んっ?計算やりなおしてみます。
> ( 温度変化によるVbe-Ic曲線を満たす点 )で収まる。これすなわちNFBによるエミッタフォロワ回路のIcの変動率の改善そのものなわけです。
なるほど、これも CV の影響をあまり受けず温度変化の影響を強く受けて Vbe1 が決まり、Vbe1 が乗った CV が Q2 にかかるという風に考えられるということでしょうか。
トランジスタ難しいですが奥が深くて面白いです。今後とも是非ご教授よろしくお願いします。
おっしゃる通り、要はVbe1が CVの変化に対してなにも影響せず、温度変化に対してのみセンサー&温度補償回路として働けばいいわけなのですが、この回路の場合おおむねそうなるという簡易版です。
この回路(エミッタフォロワ部分)の出力は R2*Ieなので当然 CVの増加にともなってIcも増加しますのでVbe1も少しは増加するわけですしVbeの値によって変化率は変わるので、厳密には入力と出力の関係はリニアな対応ではないです。
でも本来はVbeとIcの関係はEXPO,なのでそれが負帰還によって大変改善された結果が出力がおおむねリニアに見えるのです。
またこの回路では温度変化に対してIcが変化しなければVbeも変化しなくなってIsの変化の行き場所がなくなってしまうので⊿Vbe=⊿Ie*R2が成り立つように Vbe, Ic供に変化することになるのでこのIcの変化率と同じ変化率分Q2のIcも変化してしまいます。
ちょっと長くてすみませんが、以下説明です。
エミッタフォロワは基本的にはbufferということを考えればCV(入力電圧)の変化に対して出力電圧としてのVe ( …Vbe2)の変化はほぼリニアに追従するはずで、
ということは Vbe1は十分バイアスがかかっている領域においてはほとんど変動しないということになるわけですが、この出力というのは R2*Ie1の変化分でもあるわけなのでIc1が増減するのだから Vbe1はそれに対応する分だけは変化するわけです。
出力がリニアつまり、Icがリニアな変化に見えてもVbeとIcの関係はEXPO.であることに変わりはありません。 一方 Vbeが大きな値にある領域ほど ⊿Vbeの変化が少なくて同じ⊿Icの変化を得られるわけす。
この回路においてIcの変化がリニアに近いのであるのならば、Vbeの値が大きい値で動作している領域ほどVbeカーブの傾きはゆるやかになるはずで、つまりこれは CVの変化がほとんどTrのB-E間に伝わらなくなるということです。
Vbe1の変化は入力電圧のリニアな上昇に対して広範囲で見れば LOG的な変化になります。 バイアスのされ方によって変化分は異なるわけですが傾きがなだらかになった状態では入力電圧(CV)の変化に対してVbeはたとえばCVの1%程度しか変化しないというようなことになるわけです。
そもそも R2*Ie1による負帰還がVbe1に対して強くかかるからこそ入力電圧に対してVbe1の変化が極端に少なくなるわけです。 この場合、負帰還というのはVbeに対しては入力電圧の直線上昇の度合いが直接かからず、小さく、かつ非線形(LOG)にしている現象なわけで、ゆうならばVbe-Ic曲線をゆっくり移動しているようなものです。 それによって本来 EXPO.の関係にある Vbe-Icの関係をリニアなように見せているわけです。
—————————–
このエミッタフォロワの面白いところはよく見ると出力を100%負帰還する回路であってこれはOPAMPのボルテージフォロワと同じ形になっています。
OPAMPのボルテージフォロワにおいて 出力電圧は AMPの裸のGAIN(オープンループゲイン)をGAINとするとGAIN/(GAIN+1)になります。 それを反転したものと入力電圧を足したものは1/(GAIN+1)になります。
この値をGAIN倍したものが出力になるわけなので 1/(GAIN+1)+GAIN/(GAIN+1)=1となりGAINが大きいほど初めの項は0に近づき後の項は1に近づくわけです。
OPAMPの場合はGAINが大変大きいという前提なので初めの項が0に近いことがバーチャルショートになるわけです。
エミッタフォロワの場合は前項がVbe、後の項がVe (… R2*Ie)に対応しています。
つまり負帰還がかかっている分だけ CVの変化がVbeには伝わらなくなる。
実際Vbeが大きな値の領域ではCVの変化に対してVbeの変化は1%程度になるわけです。エミッタフォロワの電流増幅率は1+hFEなのでそこらへんが関連しているのでしょう。
よってこのエミッタフォロワ回路はOPAMPのボルテージフォロワの簡易版なので性質は受け付いているわけですが AMPの裸のゲインに相等する値が小さいので性能は
落ちるわけです。このゲインが大きければ 原理的にはVbeの変動もIcの変化も最小におさまるわけです。
Icが定電流ドライブされればIcの変化が最小でも定電流源のインピーダンスは非常に大きいので温度でVbeが変化しても上記の
⊿Vbe=⊿Veの関係のつじつまは合うわけです。
温度によるIsの変化をゲインの変動と考えるとゲインが非常に大きい値にあるのであれば多少ゲインが変動しても出力はほとんど影響を受けなくなるはずです。 出力電圧=GAIN/(GAIN+1)なので。
Tr 1個の動作の説明でも大変ですね。
間違えました。
>この値をGAIN倍したものが出力になるわけなので 1/(GAIN+1)+GAIN/(GAIN+1)=1となり
訂正——–>
真の入力電圧としての
1/(GAIN+1) に GAIN をかけたものが=1でありかつ
1/(GAIN+1) + GAIN/(GAIN+1)=1
となるのでGAINが大きいほど初めの項は0に近づき後の項は1に近づくわけです
すいませんまた間違えました。
エミッタフォロワのTrをNPNの
つもりで書いてしまいました。
図の回路ではPNPなのでCVの増加
でVbeが減少、Icも減少ですね。
上の説明はNPN Trだと思ってください。
何度もすみません。 また間違ってました。
電流増幅率 云々….というのは関係ないですね。
裸のゲインに影響する要素は単純には gmの値(… ⊿Ic/⊿Vbe)と
R2つまり gm*R2ですね。
だからgmが大きくなる領域ほど負帰還の効果が強くなり入力電圧の変化
と出力電圧の変化が近くなる。たとえばIc=0.1mAでR2=100Kだとすると
gm=(q/KT)*Ic=38.4Icなので38.4*0.1*10^-3 *100*10^3=380
です。
ちなみにVbeの温度係数は
-2mV/℃ で Vbeを固定できればIcの方が8%上昇します。
Ic=Is*EXP(q*Vbe/KT)の式で q/KT=1/26mvとして⊿Vbe=2mV
を入れれば1.08になります。
Vbeが18mV変化すればIcは2倍変化ですから 9℃の上昇で2倍ですが。
説明のおかしいところがありました。 毎度毎度すみません。
> このゲインが大きければ 原理的にはVbeの変動もIcの変化も最小におさまるわけです。
> Icが定電流ドライブされればIcの変化が最小でも……..⊿Vbe=⊿Veの関係のつじつ
> まは合うわけです。
このゲインが大きければ 原理的にはVinの変化に対するVbeの変動も温度変化に対するIcの変化も最小におさまるわけです。
ここまではいいとしてそれ以後の文は何を勘違いしたのか混同したのか言っていることがめちゃくちゃです。 すみません。
温度変化に対してIcの変化が小さくなる為にはVinの値が同じならR2の値が結果的に高いほうがよいということを言いたかったようです。
この回路の裸のゲインに関係するのは R2とgmなので結局 gmはIcが大きい方が大きいので R2*Ieが大きい方がよいのですが R2を大きくするとIeも下がるのですが、 R2を2倍にしてもIeは1/2より大きいので結局 R2の値が大きい方がゲインは大きくなります。 当然Vinが大きい方がゲインは大きくなりますのでVinが大きくR2が大きい方が温度変化に対するIcの変動が小さいということでしょうか。
温度変化に対して ⊿Vbe=⊿R2*Ieが成り立って Icの変化が小さくなればなるほどVbeの変化は大きくならなければならない ( つまりIcを定電流駆動した時の温度変化に対するVbeの変化に近づく) のでR2が大きくならないとつじつまが合わないということをいいたかったようです。 文章だけで説明するのはなんかむずかしいですね。
KT さん詳細なコメントありがとうございます。
ここしばらく家族サービスのためネズミーランドに行ってきたり VCF の製作に没頭していたりで申し訳ないことにまだコメント読めてません。こんどの週末ぐらいにきっちり読んで理解したいと思います。(あっ今週末花見だ!)
うだうだと冗長に書いてしまいました。 だいぶ反省しています。
暇ができたら読んでやってください。(大枠は間違っていないと思いますが…)
温度変化に対する図的な解釈としては、温度変化前のVbe-Ic曲線と、温度変化後のVbe-Ic曲線を用意してそれに対してVin=Vbe+R2*Ieを Vbe=X, Ic=Yとした時の Y=-(X+Vin)/R2という直線との交点に温度変化前の Vbe,Ic、温度変化後のVbe,Icの値があると言うだけのことです。(この直線が水平なら定電流ドライブ)
CVに対するVbeの変化の説明がくどいのはアナログ機能回路においてはこのIcとVbeの関係、Ic=Is*EXP(Vbe/VT) や 負帰還というのがマジックを演出する際の重要な要素なのであえてくどく書いてしまいました。
すいませんまた書き間違ってました。
>真の入力電圧としての
1/(GAIN+1) に GAIN をかけたものが=1でありかつ
真の入力電圧としての
1/(GAIN+1) に GAIN をかけたものが=実際のゲイン
です。