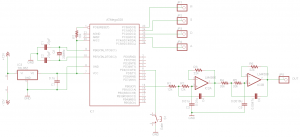
I’ve been working on implementing Envelope Generator into microprocessors. Output of an Envelope Generator consists of rising and falling exponential curve. I’m currently doing table lookup to generate those curves.

https://github.com/naokiiwakami/vceg

This is a quick and straightforward approach, and you don’t have to be worried much about data resolution. But the program is a little complicated, and memory consuming. I don’t really like this approach. I don’t really like the approach, so I started to think about alternative approaches.

Mathematically, a exponentially decaying curve can be calculated recursively by following formula:

V(i+1) = V(i) * k

where 0 <= k < 1

This is very simple. You can program this such as:

double value = INITIAL_VALUE;
double decay_factor = 0.99309249543703590153321021688807;
while (true) {
  value *= decay_factor;
}

but implementing the algorithm into a microprocessor is not straightforward like this.

I’m planning to use an AVR (e.g. atmega168), it has limited number of registers, and floating point multiplication is generally slow in AVR. So I would like to avoid floating point data types.

So shall I go for simple integer calculation? It’s actually not feasible. For example, if I update the value in every 10ms (100 updates per second) and would like to make a decaying curve that reduces its value to 50% after 1 second, the decay factor k would be

k = 0.5 ^ (1 / 100) = 0.99309249543703590153321021688807

It’s less than 1 so cannot be expressed by an integer.

There’s a technique called fixed point multiplication. This fundamentally uses integers but can handle fractions. This is my first time to try this technique, so learned how you do it. I found following link a good instruction:

https://www.allaboutcircuits.com/technical-articles/multiplication-examples-using-the-fixed-point-representation/

Tried to write it in C.

#include <stdio.h>
#include <stdint.h>

int main(int argc, char *argv[]) {
  // fixed point integer 10bit.6bit
  uint16_t value = (1023) << 6;
  // fixed point integer .16bit
  uint16_t decay_factor = 0.99309249543703590153321021688807 * 65536;
  for (uint16_t i = 0; i < 1000; ++i) {
    // multiplication
    uint32_t temp = value * decay_factor;
    value = temp >> 16;
    // retrieve the integer part
    uint16_t output = value >> 6;
    printf("%d %d\n", i, output, 10);
  }
  return 0;
}

Ran it on my PC (not on the microprocessor yet). Plotted the result to a graph:

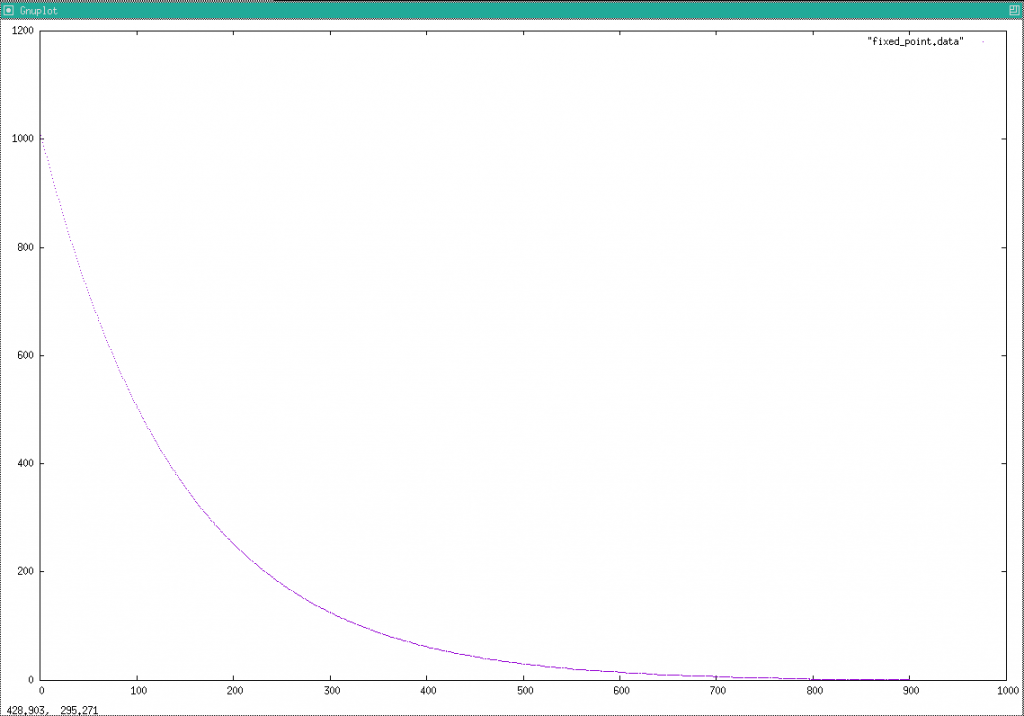
OK it looks good so far.